I-ViT Integer-only Quantization for Efficient Vision Transformer Inference

This article is review and derivation of Li et al., I-ViT: Integer-only Quantization for Efficient Vision Transformer Inference. 2023

Introduction

Vision Transformers(ViTs) have recently achieved great success on a variety of computer vision tasks.

Nevertheless, ViTs suffer from higher memory footprints, computational overhead and power consumption, hindering them deployment and real-time inference on edge devices.

• Thus, compression approaches for ViTs are being widely researched

Model quantization, which reduces the representation precision of weight/activation parameters, is an effective and hardware-friendly way to improve model efficiency.

Previous work(1) presents the dyadic arithmetic pipeline to realize integer-only inference, where the quantize the weights through the integer multiplication and bit shifting.

• This enables the quantized models to fully benefit from the fast and efficient low-precision integer arithmetic units and thus provides promising speedup effects.

However, this pipeline is designed for Convolutional Neural Network(CNN) and works under the homogeneity condition,

• Only applicable to linear(e.g., Dense) or piecewise linear(e.g., ReLU) operation

Therefore, the non-linear operation(e.g., Softmax, Gaussian Error Linear Unit(GELU) and LayerNorm) in Vision Transformer(ViT) cannot naively follow it.

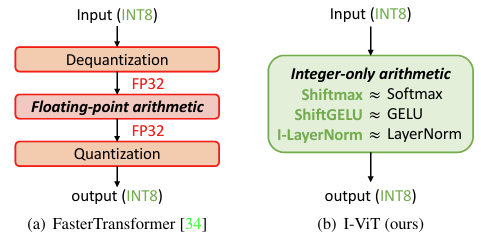
• Previous works such as FastTransformer simply leave the non-linear operation as dequantized floating-point arithmetic and makes them tolerate the inefficiency of floating point arithmetic unit, and low-cost integer only hardware cannot meet mixed-precision computing requirements.

Figure 1. Computation flows of Softmax, GELU, and LayerNorm in FasterTransformer and our proposed I-ViT. I-ViT realizes the entire computational graph with integer-only arithmetic, which is more promising and practical for low-cost model deployment and efficient inference.

Consequently, integer-only arithmetic for non-linear operations is significant for low-cost deployment and efficient inference.

However, how to accurately perform the non-linear operations of ViTs with efficient integer-only arithmetic remains an open issue.

In this paper, we propose I-ViT, which quantizes the entire computational graph to fill the research gap of integer only quantization of ViTs.

• Non-linear operations are approximated without accuracy drop by novel light-weight integer only arithmetic methods
• Shiftmax and shiftGELU perform most arithmetic with bit shifting, and I-LayerNorm calculates the square root with integer iterations instead

(1) Benoit Jacob et al., Quantization and training neural networks for efficient integer-arithmetic-only inference. In Proceeding of the IEEE conference on computer vision and pattern recognition, 2018

Related Works

Vision Transformer

Dosovitskiy et al., 2020

• ViT is first effort to apply transformer-based models to vision applications and achieves high accuracy than CNNs on the classification tasks

Touvron et al., 2020

• Data efficient image Transformer(DeiT) introduces an efficient teacher-student strategy via adding a distillation token, reducing the time and data cost in the training phase

Liu et al., 2021

• Swin presents shifted window attentions at various scales, which boost the performance of ViTs

Despite the promising performance, ViTs’ complicated architectures with large memory footprints and computational overheads is intolerable in real-world applications, especially in time/resource-constrained scenarios

Vision Transformer Quantization

Zhexin Li et al., 2022

• Quantization Vision Transformer(Q-ViT) Differentiable quantization for ViTs, taking the quantization bit-widths and scales as learnable parameters

Yang Lin et al., 2021

• Fully Quantized Vision Transformer(FQ-ViT) introduces power-of-two scale quantization and log-int quantization for LayerNorm and Softmax, respectively

Zhikai Li et al., 2022

• Patch Similarity Aware Quantization(PSAQ-ViT) pushes the quantization of ViTs to data-free scenarios based on the patch similarity

Integer-only pipeline

Yao et al., 2021

• Dyadic arithmetic is proposed to perform the integer-only pipeline for CNNs

• Designed for linear and piecewise linear operations based on the homogeneity condition, and thus is not applicable to non-linear operations in ViTs

• Several studies are interested in how to achieve integer arithmetic for non-linear operations in language Transformer models
  • Lin et al., 2020
    • Fully-8bit introduces L1 LayerNorm, which avoids the non-linearity of solving for the square root when calculating the standard deviation
  • Kim et al., 2021
    • Interger only BidERectional Transformer(I-BERT) focuses on integer polynomial approximations for the non-linear operations, including Softmax, GELU, and LayerNorm
    • The computation of high-order polynomials in inefficient in inference, and they are developed for language models that do not fit the data distribution of ViTs
    • Integer-only quantization for ViTs are remains a research gap

Methodology

The main body of ViTs is a stack of blocks, and each block is divided into a Multi-head Self-Attention(MSA) module and a Multi-Layer Perceptron(MLP) module

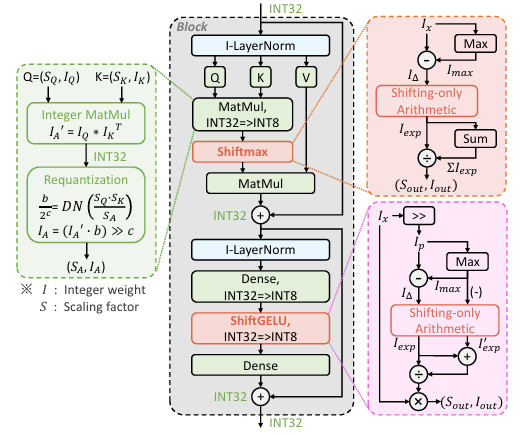
Overview of the proposed I-ViT. The entire computational graph is performed with integer-only arithmetic, wherelinear MatMul and Dense operations follow the dyadic arithmetic pipeline and the proposed Shiftmax, ShiftGELU, and I-LayerNorm accomplish the non-linear operations. Except for the labeled INT32, the remaining data streams are all INT8 precision.

MSA and MLP module can be formulated as follows

• $\hat{X} = MSA(LayerNorm(X))+X$
• $Y=MLP(LayerNorm(\hat{X}))+\hat{X}$

The MSA module learns inter-patch representations by calculating the global attention

• $MSA(X) = Concat(Attn_1, Attn_2,…,Attn_h)W^O$, where $Attn_i = Softmax(\frac{Q_i\cdot K_i^T}{\sqrt{d}})V_i$
• Query, key and value are obtained by linear projection, $Q_i=XW_i^Q, K_i=XW_i^K, V_i=XW_i^V$

The MLP module employs two dense layers and a GELU activation function to learn high-dimensional representations as follows

• $MLP(\hat{X})=GELU(\hat{X}W_1+b_1)W_2+b_2$

We apply simplest symmetric uniform quantization as follows

• $R\approx S\cdot I$, where $I=\lfloor \frac{clip(R,-m,m)}{S} \rceil, S=\frac{2m}{2^k-1}$
• Where $R$ and $I$ denote the floating point values and the quantized integer values, respectively
• $S$ is the is the scaling factor of quantization, $k$ is the quantization bit-precision, and $\lfloor \rceil$ is the round operator
• m is the clipping value determined by the min-max method, $m=\max(\left\vert R\right\vert)$

To avoid dequantization and achieve integer-only inference, we apply the dyadic arithmetic pipeline for linear operations

• Since this is based on the homogeneity condition, $Matmul(S_Q\cdot I_Q, S_K\cdot I_K)=S_Q\cdot I_Q \cdot Matmul(I_Q,I_K)$, it is not applicable to the case of non-linearity, e.g., $Softmax(S_A \cdot I_A) \neq S_A \cdot Softmax(I_A)$

Dyadic arithmetic for linear operations

The dyadic arithmetic pipeline, which uses integer bit-shifting to efficiently realize floating-point operations of scaling factors, allow linear operations to be performed with integer-only arithmetic

When the inputs are $Q=(S_Q,I_Q)$ and $K=(S_K, I_K)$, the attention matrix is calculated as follows:

• $A’= S_Q\cdot S_K\cdot (I_Q \times I_K^T)$, where $I_Q \times I_K^T$ performs integer-only arithmetic

However, $I_Q \times I_K^T$ can exceed INT8 range, so we need to requantize as follows

• $A=S_A\cdot I_A$, $I_A=\lfloor \frac{A’}{S_A} \rceil=\lfloor \frac{S_Q\cdot S_K}{S_A}\cdot (I_Q\times I_K^T) \rceil$, where $S_A=\frac{2m}{2^k-1}, m=\max(\left\vert A’\right\vert)$
• Multiplication and division of scaling factors can be avoided by converting the rescaling to a dyadic number as follows: $DN(\frac{S_Q\cdot S_K}{S_A})=\frac{b}{2^c}$
• To summarize, the integer-only arithmetic pipeline of MatMul can be denoted as follows: $I_A=(b\cdot (I_Q\times I_K^T))\gg c$

Dyadic number algorithm

Brute force dyadic number conversion algorithm

def to_dyadic(x,max_precision=10):
    best_error = float('inf')
    best_b = 0
    best_c=0
    for c in range(max_precision+1):
        b = round(x * (2 ** c))
        error = abs(x - b / (2 ** c))
        if error < best_error:
            best_error = error
            best_b = b
            best_c = c
        if error == 0:
            break
    return (best_b, 2**best_c)

Stern-Brocot tree algorithm

Figure 11. Stern-Brocot tree algorithm

ref: https://en.wikipedia.org/wiki/Stern%E2%80%93Brocot_tree

Integer-only Softmax - Shiftmax

Softmax in ViTs translates the attention scores into probabilities and is calculated as follows:

• $Softmax(x_i)=\frac{e^{x_i}}{\sum_{j=1}^d e^{x_j}}=\frac{e^{S_{x_i}\cdot I_{x_i}}}{\sum_{j=1}^d e^{S_{x_j}\cdot I_{x_j}}}$

Due to the non-linearity, softmax cannot follow the dyadic arithmetic pipeline and the exponential arithmetic is typically unsupported by integer-only logic unit

We propose the approximation method shiftmax, which can achieve accurate and efficient integer-only arithmetic of softmax

First, to smooth the data distribution and prevent overflow, we restrict the range of the exponential arithmetic as follows:

• $Softmax(x_i)= \frac{e^{S_{\Delta_i}\cdot I_{\Delta_i}}}{\sum_{j=1}^d e^{S_{\Delta_j}\cdot I_{\Delta_j}}} = \frac{e^{S_{x_i}\cdot (I_{x_i}-I_{max})}}{\sum_{j=1}^d e^{S_{x_j}\cdot (I_{x_j}-I_{max})}}$
  • Where $I_{max} = max(I_{x_1},I_{x_2},…,I_{x_d})$, $\therefore I_\Delta \leq 0$

Convert the base from $e$ to 2 to fully utilize the efficient shifters

• Since $\log_2 e$ can be approximated by binary as $(1.0111)_2=(1.1)_2-(0.0001)_2$, the floating-point multiplication with it can be achieved by integer shifting as follows:
• $e^{S_\Delta \cdot I_\Delta}=2^{S_\Delta \cdot (I_\Delta \cdot \log_2 e)}\approx 2^{S_\Delta \cdot (I_\Delta+(I_\Delta \gg 1)-(I_\Delta \gg 4))}$
• $\because \log_2 e \approx 1.4427 \approx 1+0.25+0.125+0.0625=1.4375$

Let $I_p=(I_\Delta+(I_\Delta \gg 1)-(I_\Delta \gg 4))$, the power term is denoted as $S_\Delta \cdot I_p$, which is not ensured as an integer

• We decompose $S_\Delta\cdot I_p $ into an integer part $-q$ and a decimal part $S_\Delta \cdot (-r)$ as follows(Note that $I_p \leq 0 \because I_\Delta=I_x - I_{max}$):

• $2^{S_\Delta \cdot I_p}=2^{(-q)+S_\Delta \cdot (-r)}=2^{S_\Delta \cdot (-r)}\gg q$
• $I_0=\lfloor \frac{1}{S_\Delta} \rceil$, $q=\lfloor \frac{I_p}{-I_0} \rfloor$, $r=-(I_p-q\cdot (-I_0))$
• $S_\Delta \cdot (-r) \in (-1,0]$
  • $\because q=\lfloor \frac{I_p}{-I_0} \rfloor \approx \lfloor -S_\Delta\cdot I_p \rfloor$
  • $\therefore S_\Delta \cdot (-r)=S_\Delta \cdot (I_p+q\cdot I_0)\approx S_\Delta \cdot I_p + (S_\Delta \cdot \lfloor -S_\Delta \cdot I_p \rfloor \cdot I_0) \approx S_\Delta \cdot I_p + \lfloor -S_\Delta \cdot I_p \rfloor$
• $2^{S_\Delta\cdot (-r)}\approx \frac{S_\Delta \cdot (-r)}{2}+1=S_\Delta\cdot((-r)\gg 1 +I_0)$
• $S_\Delta \cdot I_{exp}=S_\Delta \cdot ((-r) \gg 1)\approx e^{S_\Delta\cdot I_\Delta}$
• For more precise derivaiton, please see Appendix

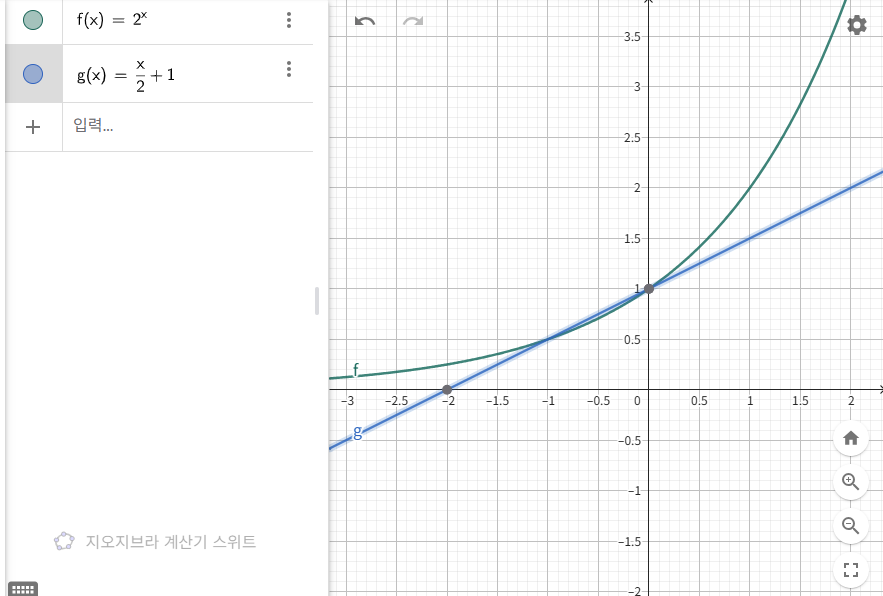
Figure 4. The graph of $y=2^x$ and $y=\frac{x}{2}+1$ we can approximate $y=2^x$ to $y=\frac{x}{2}+1$ when $-1<x\leq 0$

If we use same scaling factor $S_\Delta$, then $Softmax(x_i)=\frac{S_\Delta\cdot I_{exp_i}}{S_\Delta\cdot \sum_{j=1}^d I_{exp_j}}$

• This turns softmax into an integer division, which is calculated with the specified output bit-precision $k_out$ as follows
• $I_{out_i}=\frac{S_\Delta\cdot I_{exp_i}}{S_\Delta\cdot \sum_{j=1}^d I_{exp_j}}=(\lfloor \frac{2^M}{\sum_{j=1}^d I_{exp_j}} \rfloor \cdot I_{exp_i}) \gg (M-(k_{out}-1))$
• $S_{out_i} = \frac{1}{2^{k_{out}-1}}$
• $M$ is a sufficiently large integer, and $S_{out_i}\cdot I_{out_i}$ can approximate the result of Softmax

Figure 3. Shiftmax algorithm

Integer-only GELU ShiftGELU

GELU is the non-linear activation function in ViTs, can be approximated by a sigmoid function as follows:

• $GELU(x)=x\cdot \Phi(x)=x\cdot \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-\frac{t^2}{2}}dt \approx x\cdot \sigma(1.702x)=S_x\cdot I_x\cdot \sigma(S_x\cdot 1.702 I_x)$

Cumulative distribution function and sigmoid function is simillar

The cumulative distribution function (CDF) gives the probability that a random variable takes a value less than or equal to a specific number. It shows how probability accumulates as the variable increases

1.702 can be approximated by binary as $(1.1011)_2$, thus $1.702I_x$ can be achieved by integer shifting, $I_p=I_x+(I_x \gg 1)+(I_x \gg 3)+(I_x \gg 4)$

We equivalently transform the sigmoid function as follows

• $\sigma(S_x\cdot I_p)=\frac{1}{1+e^{-S_x\cdot I_p}}=\frac{e^{S_x\cdot I_p}}{1+e^{S_x \cdot I_p}}=\frac{e^{S_x\cdot (I_p - I_{max})}}{e^{S_x\cdot (-I_{max})}+e^{S_x\cdot (I_p-I_{max})}}$, and the subsequent process is the same as shiftmax

Figure 5. Gaussian Distribution

Figure 6. Cumulative Distirbution Function

Figure 7. Sigmoid function

Figure 3. ShiftGELU algorithm

Integer-only LayerNorm I-LayerNorm

LayerNorm in ViTs normalizes the input in the hidden feature dimension as follows

• $LayerNorm(x)=\frac{x-Mean(x)}{\sqrt{Var(x)}}\cdot \gamma +\beta$
• $\frac{x-Mean(x)}{\sqrt{Var(x)}}=\frac{S_x\cdot I_x-S_x Mean(I_x)}{S_x \sqrt{Var(I_x)}}=\frac{I_x-Mean(I_x)}{\sqrt{Var(I_x)}}$
• Where $\gamma$ and $\beta$ are linear affine factors
• Layernorm needs to dynamically compute statistics(mean and standard deviation) in the inference phase
• Integer arithmetic units allow straight forward calculation of the mean and variance of the data, yet they fail to support the square root
• Thus, we improve the light-weight integer iterative approach for square root via bit-shifting as follows
• $O_{i+1}=(O_i+\lfloor \frac{Var(I_x)}{O_i} \rfloor)\gg 1, O_0=2^{\lfloor bit(Var(I_x)/2) \rfloor}$
  • Newton-Raphson method
• We experimentally find that 10 iterations can achieve most convergence

Newton-Raphson method for integer square root

def newton_sqrt(x, max_iter=10):
    if x < 0:
        raise ValueError("Cannot compute square root of negative number")
    if x == 0:
        return 0
    guess = 2**(math.floor(x.bit_length() / 2))
    for _ in range(max_iter):
        guess = (guess + math.floor(x / guess)) >>1

Experiments

I-ViT is compared end-to-end with the following methods

• FastTransformer that leave non-linear operations as floating point arithmetic
• I-BERT that approximate non-linear operations with integer second order polynomials

Accuracy evaluation

• I-ViT is evaluated on various popular models, including ViT, DeiT and Swin on ImageNet(ILSVRC-2012) dataset
• First, we quantize the weights of the pre-trained model, then we perform quantization-aware fine-tuning using naïve Straight Through Estimator(STE) to recover the accuracy

Latency evaluation

• We deploy I-ViT on an Ray Tracing texel eXtreme(RTX) 2080Ti Graphic Processing Unit(GPU)to measure real hardware latency
• Although the GPU is not an integer-only hardware, depending on the Dot Product of four 8-bit integers with 32-bit Accumulate(DP4A) instruction, I-ViT can perform efficient integer-only inference on its Turing tensor cores

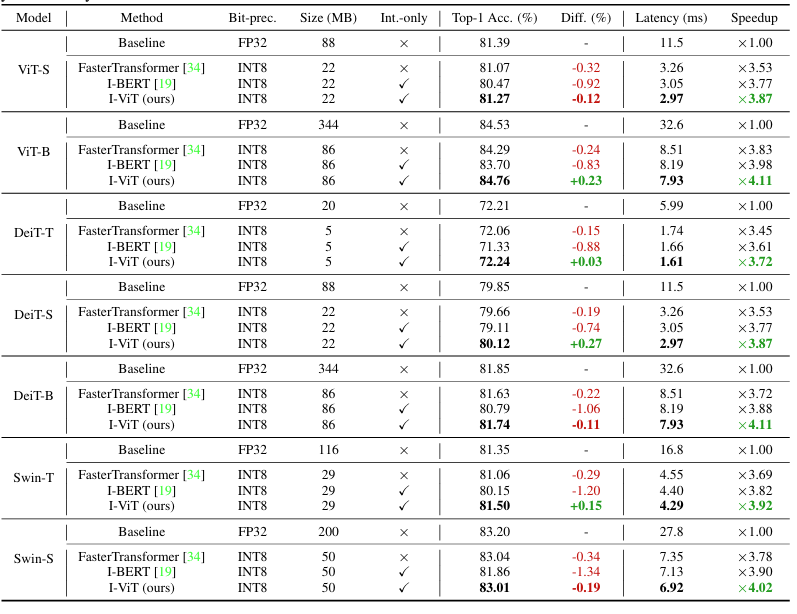
Accuracy and latency results

Table1.Accuracy and latency results on various model benchmarks. Here, accuracy is evaluated on ImageNet dataset, and latency is evaluated on an RTX2080Ti GPU(batch=8). Compared to the FP baseline, I-ViT, which quantizes the entire computational graph and enables integer-only inference on Turing Tensor Cores, can achieve similar or even slightly higher accuracy and provides a significant 3.72-4.11x speedup. In addition, I-ViT consistently outperforms existing works FastTransformer and I-BERT in terms of both accuracy and latency

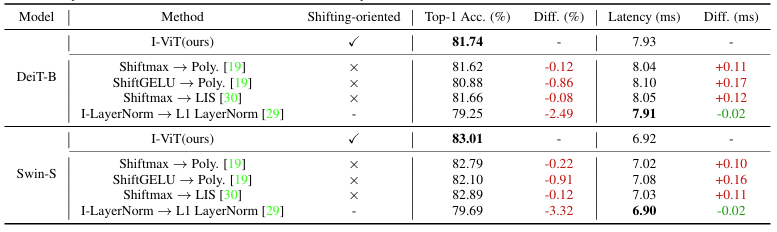
Ablation Studies

Comparision with other quantization

• Second-order polynomial approximation in I-BERT
• Log-Int-Softmax(LIS), which builds upon I-BERT and adds the logarithmic function in FQ-ViT
• L1 LayerNorm, which uses L1 norm to replace the calculation of standard deviation in Fully-8bit

Table 2. Ablation studies of accuracy and latency of Shiftmax, ShiftGELU and I-LayerNorm. Latency is evaluated on an RTX 2080Ti GPU(batch=8), REplacing Shiftmax and ShiftGELU with second-order polynomial approximations leads to lower accuracy and higher latency, and L1-LayerNorm suffers from non-trivial accuracy loss due to the mismatch in the data distribution and low approximation capability

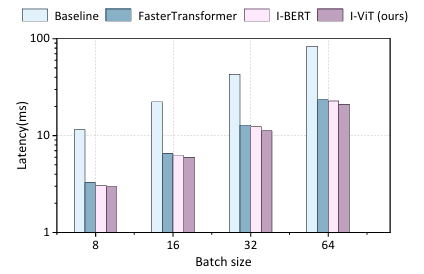
Evaluate the latency of DeiT-S with various batch size

• I-ViT is robust to the batch size and can maintain a constant acceleration effect
• There is no full parallelism after increasing the batch size results in a corresponding increase in latency
• Deploying I-ViT on dedicated hardware like Filed Programmable Gate Array(FPGA) will further enhance the acceleration potential

Figure 9. Latency results of DeiT-S evaluated on an RTX2080Ti GPU with various batch size. I-ViT maintains a constant acceleration effect for the sam emodel architecture at various batch sizes

Conclusion

In this paper, we propose I-ViT, which is the first integer-only quantization scheme for ViTs to the best of our knowledge

I-ViT quantizes the entire computational graph to enable the integer-only inference, where linear operations follow the dyadic arithmetic pipeline Non-linear operations are performed by the proposed novel light-weight integer-only approximation methods

Compared to the floating point baseline, I-ViT achieves similar accuracy on various benchmarks Additionally, I-ViT achieves a 3.72-4.11 speedup over the baseline model on RTX 2080Ti

In the future, we will consider deploying I-ViT on FPGA, and furthermore, we also plan to extend I-ViT to more complex vision tasks like object detection and semantic segmentation

References

Zhikai Li, Qingyi Gu, “I-ViT: Integer-only Quantization for Efficient Vision Transformer Inference,” 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2023, pp. 17019-17029

Appendix

Derivation of $S_\Delta \cdot (-r)\in (-1,0]$

• $S_\Delta \cdot (-r)=S_\Delta \cdot (I_p+q\cdot I_0)=S_\Delta \cdot I_p + S_\Delta \cdot q \cdot I_0$
• $q \leq -\frac{I_p}{I_0} < q+1 ,\because q=\lfloor \frac{I_p}{-I_0} \rfloor$
• From $q \leq -\frac{I_p}{I_0}$, $I_p+q\cdot I_0 \leq 0$, $\therefore S_\Delta \cdot (I_p+q\cdot I_0) \leq 0$
• From $-\frac{I_p}{I_0} < q+1$, $I_p+q\cdot I_0 > -I_0$, $\therefore S_\Delta \cdot (I_p+q\cdot I_0) > -S_\Delta \cdot I_0$
  • $\because I_0 \leq \frac{1}{S_\Delta} <I_0+1$, $\therefore S_\Delta \cdot I_0 \leq 1$
• $\therefore S_\Delta \cdot (-r)\in (-1,0]$

STE

• Technique used in neural networks to handle non-differentiable functions during backpropagation
• It approximates gradients by using the identity function(gradient=1) or copying gradients from the forward pass, allowing gradient flow through non-differentiable operations

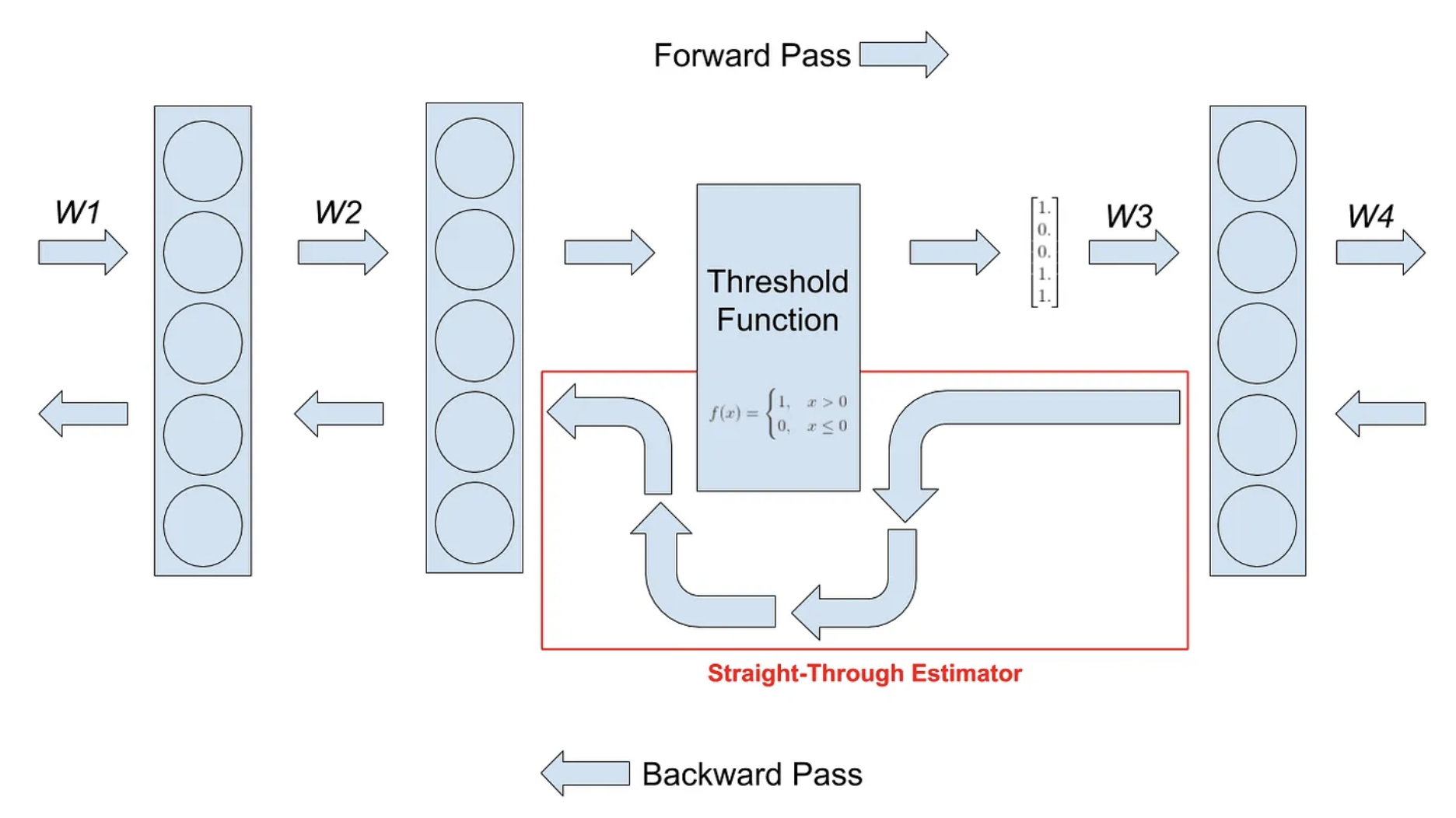
Figure 13. Straight-through estimator

I-ViT code on Github

https://github.com/zkkli/I-ViT